On Thursday the 22nd of October 2002 I presented a work titled Dynamic Partial Correlation Models at the VU Econometrics BrownBag Seminar.
This is a working paper that I am currently developing with professor André Lucas (you can check out the poster here, that we presented earlier this year at the 2022 NESG Conference in Groningen) or take a look at the presentation (here).
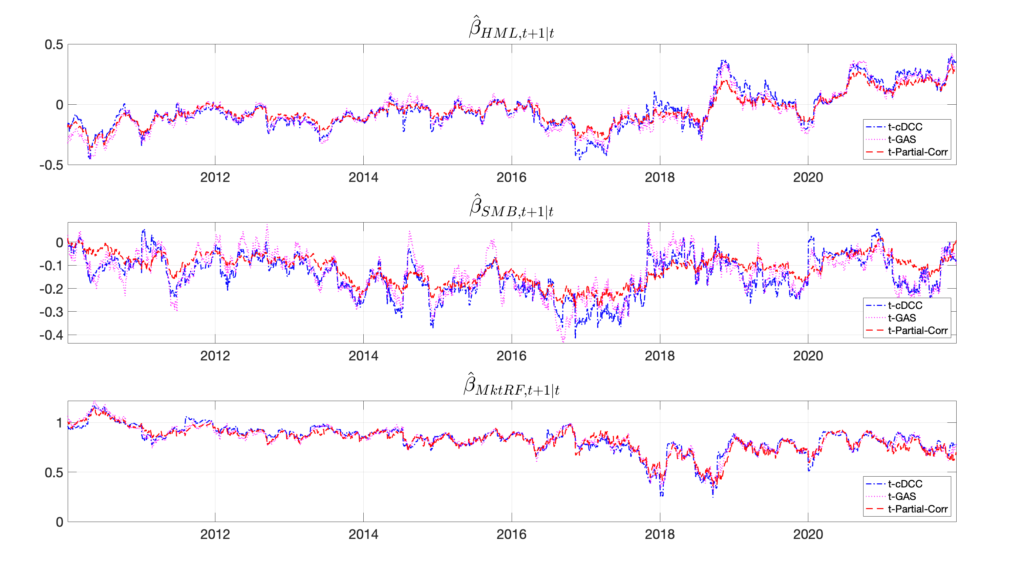
In this paper we introduce a new nonlinear dynamic model for dynamic conditional correlation matrices. To generate correlation matrices that satisfy the constraints of positive (semi) definiteness and ones on the diagonal, we parameterize the correlation matrix using a sequence of partial correlations. Each partial correlation is built recursively from previous partial correlations and pairwise correlations using the so called D-vine copula structure as introduced by Joe (2006) in a static framework for random correlation matrices. The main advantages of this strategy are that:
i) it ensures positive definite correlation matrices with a sequence of simple transformations (rather than a more involved one like the log-correlation matrix or the hypersphere coordinates);
(ii) the method is easily scalable to higher dimensions without loosing computational stability (which off-sets it from other parameterizations);
(iii) the recursive structure of the parameterization allows for much a much simplified asymptotic analysis of the process and the maximum likelihood estimator;
(iv) the formulation allows us to easily impose (theoretical) restrictions such as zero restrictions on some of the partial correlations during the filtering stage.
We allow for both Gaussian and Student’s t distributions.
We provide conditions for stationarity, ergodicity and invertibility of our model and prove strong consistency and asymptotic normality of the maximum likelihood estimator.
In an extensive Monte Carlo simulation and in an empirical in-sample and out-of-sample analysis of stock return data we find that the new approach outperforms a range of recent alternatives, including the (classic) DCC model introduced by Engle (2002) and
by Aielli (2013), the GAS correlation model of Creal et al. (2012).
Please feel free to leave a comment below or contact me if you’re interested in some more details. Your feedback is always greatly appreciated.